Understanding LQR: A Comprehensive Guide To Linear Quadratic Regulator

In the field of control systems, Linear Quadratic Regulator (LQR) has emerged as a fundamental concept that significantly enhances system stability and performance. This article delves into the intricacies of LQR, its applications, and its significance in modern engineering. Whether you are a student, an engineer, or simply curious about control theory, this guide aims to provide valuable insights into the world of LQR.

The Linear Quadratic Regulator is a type of optimal control strategy widely used in various engineering fields. By minimizing a quadratic cost function, LQR ensures that the system behaves in the desired manner while maintaining efficiency. This article will equip you with a thorough understanding of LQR, its mathematical foundations, and its practical applications across different industries.

As we explore LQR, we will cover essential topics such as its definition, advantages, mathematical formulation, and real-world applications. Additionally, we will provide valuable examples and data to support our discussion, ensuring that you have a comprehensive understanding of this critical control strategy.

Table of Contents

• What is LQR?
• Mathematical Formulation of LQR
• Advantages of LQR
• Applications of LQR
• LQR in Robotics
• LQR in Aerospace
• LQR and Autonomous Vehicles
• Future of LQR

What is LQR?

The Linear Quadratic Regulator (LQR) is an optimal control strategy used in the field of control theory. It is designed to operate linear dynamic systems while minimizing a cost function that typically consists of state variables and control inputs. The primary goal of LQR is to achieve a balance between performance and control effort.

In essence, LQR formulates a control law that provides the best possible control input to a system based on its current state. By employing a state feedback mechanism, LQR can stabilize the system and ensure that it responds optimally to various disturbances.

Key Features of LQR

• Optimal control strategy for linear systems.
• Minimizes a quadratic cost function.
• Utilizes state feedback for system stabilization.
• Widely applicable across various engineering domains.

Mathematical Formulation of LQR

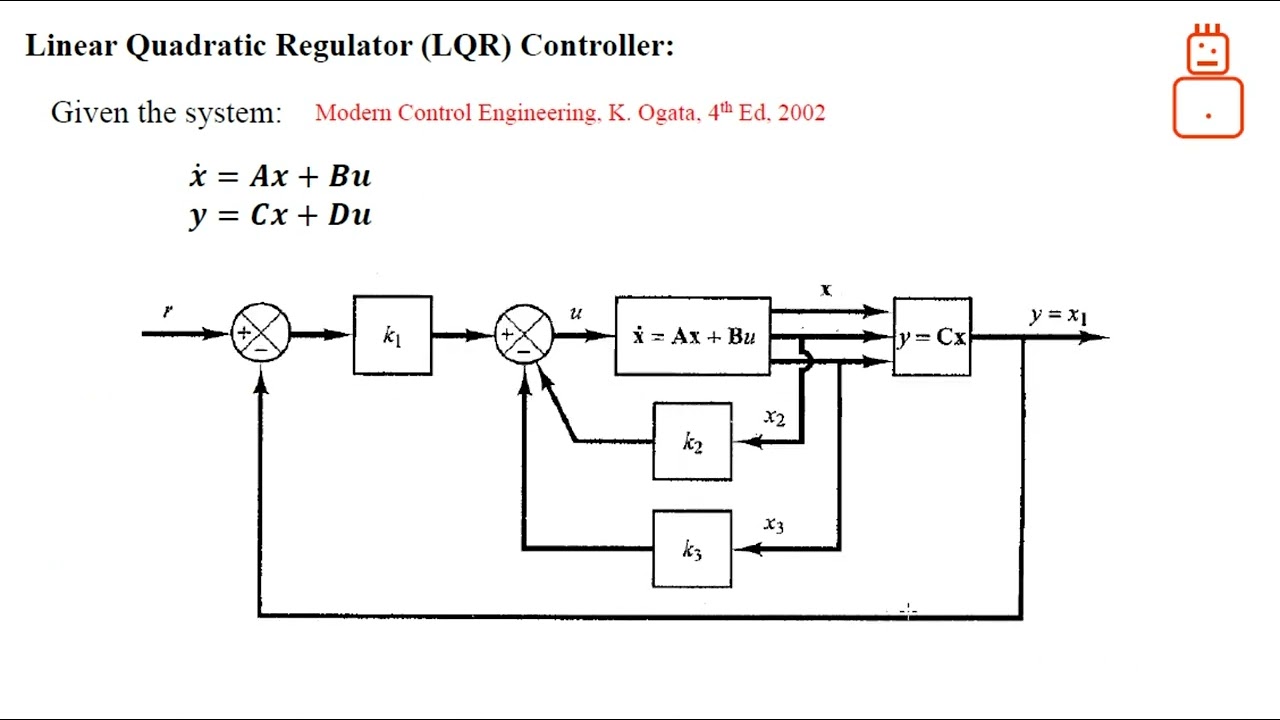
The mathematical formulation of LQR involves the definition of a state-space representation of the system. This representation is expressed in the form of linear differential equations. The state-space model can be described by the following equations:

1. State equation:
$$\dot{x}(t) = Ax(t) + Bu(t)$$

2. Output equation:
$$y(t) = Cx(t) + Du(t)$$

Here, \(x(t)\) represents the state vector, \(u(t)\) is the control input, and \(A\), \(B\), \(C\), and \(D\) are system matrices.

To achieve the optimal control input \(u(t)\), LQR minimizes the following quadratic cost function:

$$J = \int_{0}^{\infty} (x^T Q x + u^T R u) dt$$

Where \(Q\) and \(R\) are weight matrices that determine the relative importance of the state and control input in the cost function. The optimal control law is given by:

$$u(t) = -Kx(t)$$

Where \(K\) is the feedback gain matrix calculated using the solution of the algebraic Riccati equation.

Advantages of LQR

LQR offers several advantages that make it a preferred choice in control system design:

• Optimal Performance: LQR guarantees optimal performance by minimizing the defined cost function.
• Robustness: The state feedback mechanism enhances the system's robustness against disturbances.
• Simplicity: LQR is straightforward to implement and can be applied to a wide range of linear systems.
• Flexibility: The choice of weight matrices \(Q\) and \(R\) allows for customization based on specific performance criteria.

Applications of LQR

LQR has found extensive applications in various fields, including but not limited to:

• Robotics
• Aerospace engineering
• Automotive systems
• Industrial automation
• Power systems

LQR in Robotics

In the field of robotics, LQR plays a crucial role in controlling robotic arms and mobile robots. By utilizing LQR, engineers can design controllers that ensure precise movement and stability in dynamic environments.

For example, in robotic arm control, LQR can be used to optimize the trajectory of the arm while minimizing energy consumption. This is achieved by defining appropriate \(Q\) and \(R\) matrices to balance performance and control effort.

LQR in Aerospace

Aerospace engineering heavily relies on LQR for flight control systems. The ability to stabilize aircraft and spacecraft during various phases of flight is paramount for safety and efficiency.

LQR is employed in autopilot systems to maintain desired flight paths and respond effectively to disturbances such as turbulence. By tuning the weight matrices, aerospace engineers can enhance the performance of the control systems.

LQR and Autonomous Vehicles

With the rise of autonomous vehicles, LQR has become increasingly relevant. The control strategies developed using LQR ensure that autonomous vehicles navigate safely and efficiently in complex environments.

LQR can be integrated with other control strategies, such as Model Predictive Control (MPC), to achieve optimal path planning and obstacle avoidance. This combination enhances the overall performance of autonomous systems.

Future of LQR

The future of LQR remains bright, as it continues to evolve with advancements in technology and control theory. Researchers are exploring new techniques to enhance LQR's capabilities, including adaptive LQR and robust LQR.

As industries increasingly adopt automation and autonomous systems, the demand for effective control strategies like LQR will only grow. Continuous research and development in this area will lead to improved performance and reliability of various systems.

Conclusion

In summary, the Linear Quadratic Regulator (LQR) is a powerful tool in control theory that optimizes system performance while ensuring stability. Its mathematical formulation, advantages, and wide range of applications make it an essential component in modern engineering. As technology advances, LQR will continue to play a vital role in the development of autonomous systems and robotics.

We encourage you to explore more about LQR and its applications. Leave a comment below, share this article with others, and stay tuned for more insightful content on control theory and engineering.

Penutup

Thank you for taking the time to read this comprehensive guide on LQR. We hope you found the information valuable and insightful. Don't hesitate to return for more articles that deepen your understanding of control systems and engineering principles.

Exploring Fallas Paredes: A Comprehensive Guide To Understanding This Unique Tradition
West Side Story Cast: A Deep Dive Into The Talents Behind The Iconic Film
How Short Is The Shortest Running Back In NFL History?